Observation of artificial satellites
On this page I report the observation of several artificial satellites on 28-Aug-2012.
On the evening of 27th August 2012 we were observing the asteroid (602) Marianna when we noticed several satellites crossing the images from East to West very slowly. The angular speed was about 0.25 deg/min so we realised quickly we were right at the position where all geostationary satellites are visible.
In 4 hours of observation we could take images of 52 geostationary satellites, plus 3 non-geostationnary crossing the field of view with different speeds and directions.
Below we show the most interesting findings. At the bottom of the page we give a few hints on the identification of the satellites.
Piece of Ariane-5 rocket
A piece of Ariane rocket (R/B = rocket body) flying in a geostationary transfer orbit (the type of orbit used to launch geostationary satellites).

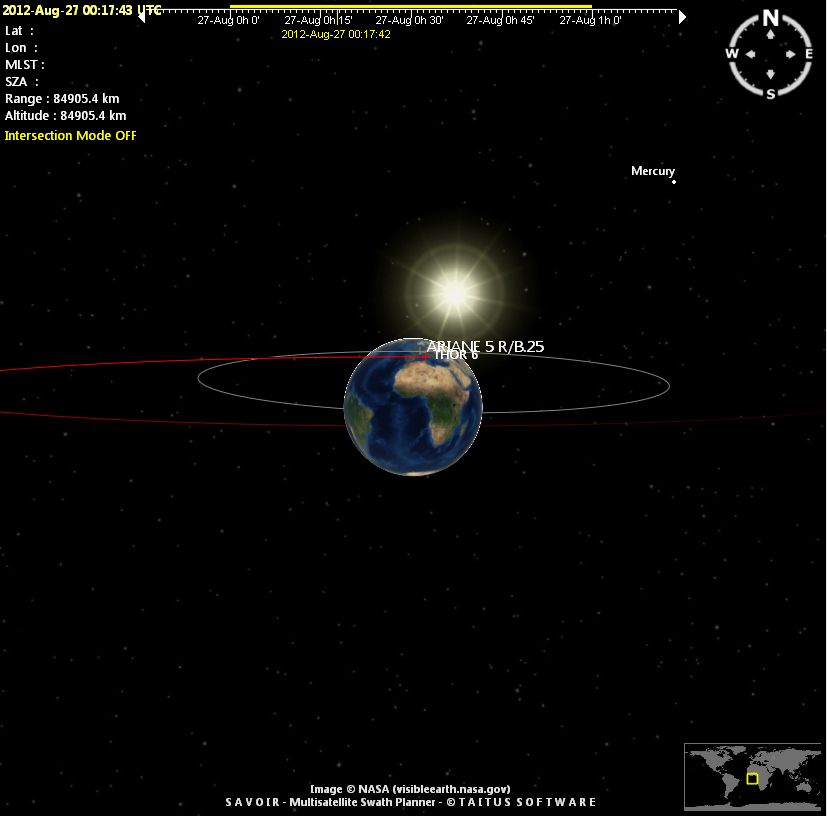
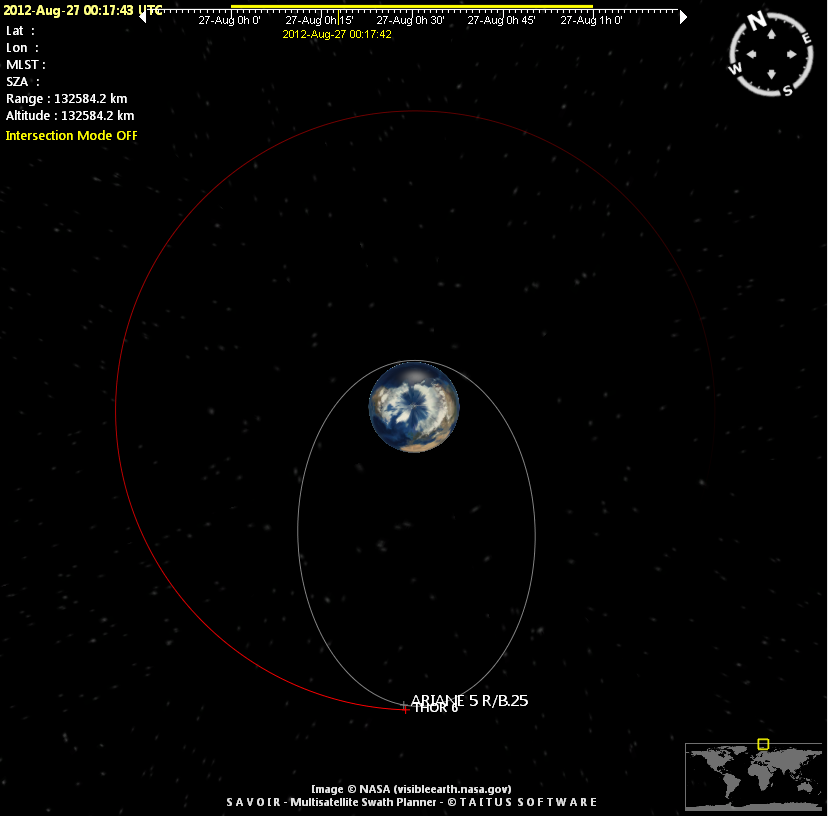 |
| Identification of GPS satellite with Savoir software |
GPS satellite
One of the GPS satellite in operation.
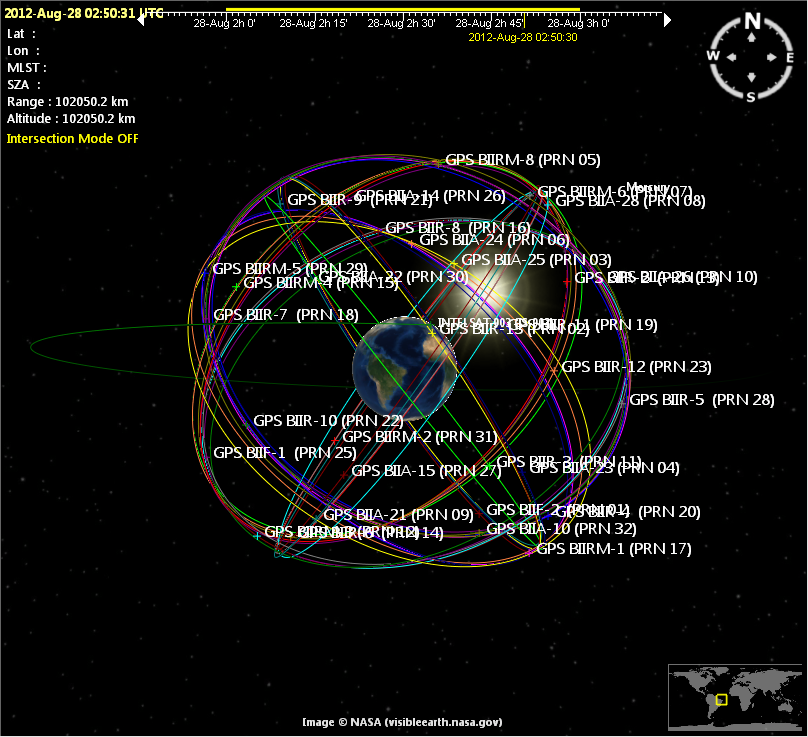
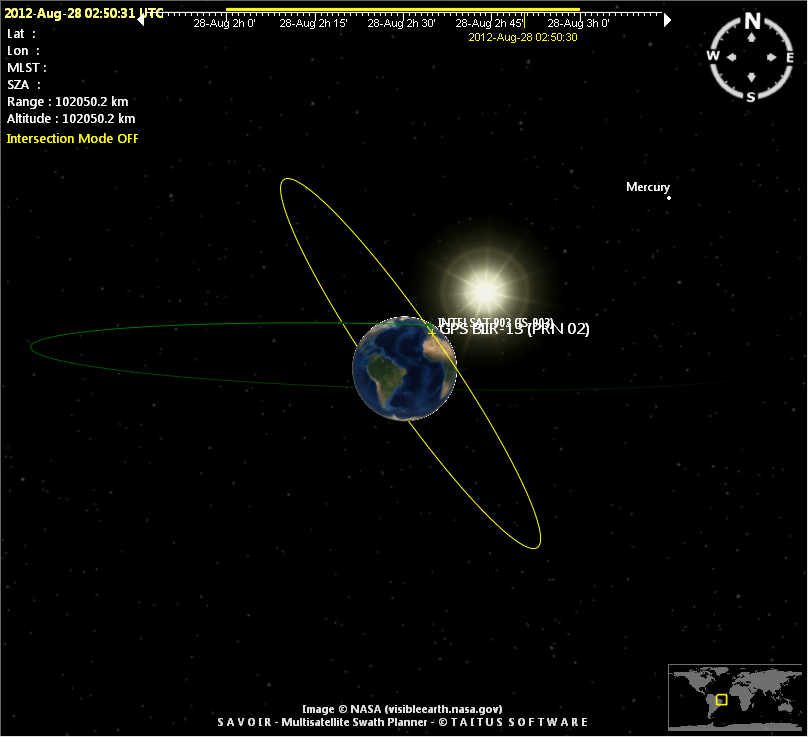 |
| Identification of GPS satellite with Savoir software |
Declination where geostationary satellites can be observed
The Dauban observatory (MPC A77) is at a positive latitude +44deg so the geostationary satellites are observed at a negative declination. The figure below illustrates this:

The declination of GEO satellites (delta) can be calculated from the latitude (phi) with:
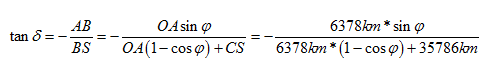
A more accurate equation, including the effect of Earth oblateness is:
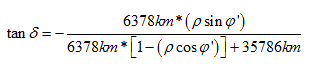
Two methods for satellite identification
To identify the satellites we used two techniques:
- we re-calculated the orbit parameters from the measured positions, assuming a circular orbit (the majority of the operating satellites is flying on circular orbits so this is a reasonable starting point). To do it we wrote a simple orbit model in Excel, and searched for 4 parameters = semi-major axis, inclination, position of ascending node, position of satellite on orbit, that allow to recalculate the 4 measured quantities = alpha, delta, angular speed, azimuthal direction of satellite. With the MS Excel solver we could obtain the orbit of most satellites like this.
- for an elliptical orbit, the angular speed of a satellite with respect to the stars (=inertial frame) and seen from the center of the Earth can vary between the following boundaries:
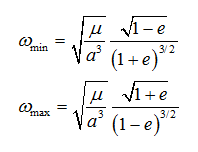
In this equation, mu is the geocentric constant of gravitation (=3.9860044 m^3/s^2), a the semi-major axis and e the eccentricity. Omega_min and omega_max are obtained in rad/sec, they must be multiplied by 180/pi ~ 57.296 to be expressed in deg/sec.
We looked at the official listings of artificial satellites (celestrack and spacetrack) and filtered the listing to keep only the satellites with values of a and e for which the angular speed observed from Dauban observatory is compatible with omega_min and omega_max. The 2 equations give the angular speed at the center of the Earth but since the satellites are far away from the Earth it should not be so different from the apparent angular speed seen at Dauban observatory. Since the satellites are far away, the filtering is very efficient and more than 95% of the satellites which fly on low altitude orbits are immediately filtered out. We also ruled out quickly the satellites with clearly incompatible values of the orbit inclination. Finally we used the demo version of Savoir to visualise the positions of the remaining satellites and find which one was actually observed.